|
|
|
|
|
|
|
Logica e arbitrio nella meccanica ondulatoria
Adriano Orefice, Raffaele Giovanelli, Domenico Ditto
26 Giugno 2013
Introduzione
Questo articolo ha lo scopo di ripercorrere alcuni punti cruciali della Fisica che si pensavano tranquillamente consegnati alla storia della scienza e delle scoperte scientifiche. Il mondo in cui viviamo ed in cui si svolgono scontri ideologici e guerre cruente con i conseguenti dibattiti, è fortemente condizionato dalle infinite applicazioni delle scoperte conseguite nel regno delle scienze del mondo fisico. Questa realtà è lontanissima dal pensiero dominante in Italia, solidamente ancorata ad una visione arcaica della realtà, in cui tutto risalirebbe a convincimenti emotivi e passionali, cioè riassunti nella sfera della politica. La filosofia di Benedetto Croce ha dato una forma ben salda a questo nostro atteggiamento in cui si sarebbe dovuto avere il primato della storia e poi, come corollario, quello della politica. Ma molte novità tecniche in campo militare e nel campo civile stanno per entrare in gioco determinando ancora nuove mutazioni nei precari equilibri mondiali. Così, per distoglierci dal torpore della nostra italica disattenzione, si propone questo articolo come una presa di coscienza della realtà costituita dalla tecnica e dalla scienza in continua evoluzione.
(N.B. Il lettore «non specialista» non si allarmi per le poche formule matematiche presenti, da intendersi molto più come pittoresche icone che come parte del racconto).
Nell’ultimo ventennio del XIX secolo Balmer e Rydberg osservarono che la lunghezza d’onda, λ, delle righe dello spettro di emissione dell’idrogeno poteva essere espressa mediante una relazione empirica semplicissima:
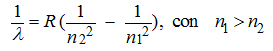 (1) (1)
ove R è un’opportuna costante, detta «di Rydberg», e n1 ed n2 sono numeri interi. La giustificazione di tale formula rimase del tutto oscura per quasi vent’anni: ma l’avventura era solo all’inizio.
 Nel 1900 un’altra ipotesi empirica «fortunata» fu avanzata, questa volta da Planck, per descrivere «lo spettro di emissione di corpo nero». Si tratta, in linea di principio, di un emettitore ideale, la cui emissione di radiazione elettromagnetica dipende solo dalla sua temperatura e non dalla sostanza di cui è fatto, né dalle proprietà della superficie. Questo emettitore, caratterizzato dal fatto di assorbire, senza alcuna riflessione, ogni radiazione elettromagnetica che vi incida, e di emettere sull’intero spettro di frequenze, viene simulato sperimentalmente creando, in un corpo reale, una cavità (le cui pareti sono mantenute a temperatura costante) che irradia all’esterno, attraverso un foro, uno spettro di radiazione che si ritiene prossimo a quello di un corpo nero ideale. Nel 1900 un’altra ipotesi empirica «fortunata» fu avanzata, questa volta da Planck, per descrivere «lo spettro di emissione di corpo nero». Si tratta, in linea di principio, di un emettitore ideale, la cui emissione di radiazione elettromagnetica dipende solo dalla sua temperatura e non dalla sostanza di cui è fatto, né dalle proprietà della superficie. Questo emettitore, caratterizzato dal fatto di assorbire, senza alcuna riflessione, ogni radiazione elettromagnetica che vi incida, e di emettere sull’intero spettro di frequenze, viene simulato sperimentalmente creando, in un corpo reale, una cavità (le cui pareti sono mantenute a temperatura costante) che irradia all’esterno, attraverso un foro, uno spettro di radiazione che si ritiene prossimo a quello di un corpo nero ideale.
Ebbene, Planck ipotizzò, con grande successo, che in tale processo l’energia possa essere emessa soltanto mediante «pacchetti» finiti e discreti, detti «quanti», con energia E legata alla frequenza V della radiazione da un’altra relazione semplicissima,
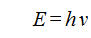 (2) (2)
ove la costante, h, detta appunto «di Planck», fu determinata dal confronto sperimentale con gli spettri osservati, e risultò essere una costante universale basilare per tutti i fenomeni microscopici. Il premio Nobel giunse a Planck nel 1918.
 La formula di Planck indusse Bohr, nel 1913, a proporre un insieme di postulati «ad hoc» che contrastavano addirittura con la teoria maxwel-liana dell’elettromagnetismo, ma da cui uscì un «modello planetario» dell’atomo che prevedeva correttamente le righe di emissione di Balmer-Rydberg e forniva anche altre importanti informazioni, come le energie di eccitazione e jonizzazione dell’atomo. La formula di Planck indusse Bohr, nel 1913, a proporre un insieme di postulati «ad hoc» che contrastavano addirittura con la teoria maxwel-liana dell’elettromagnetismo, ma da cui uscì un «modello planetario» dell’atomo che prevedeva correttamente le righe di emissione di Balmer-Rydberg e forniva anche altre importanti informazioni, come le energie di eccitazione e jonizzazione dell’atomo.
Il modello atomico di Bohr (che fu detto «semi-classico», per la bizzarra coalescenza di Fisica Classica e ricette empiriche, e che fruttò a Bohr il premio Nobel nel 1922) era l’epìtome di un metodo di ricerca, che potremo definire «di arbitrio fortunato», che lasciava ai ricercatori il dovere morale di far rientrare il tutto, prima o poi, in una teoria fisica coerente.
Purtroppo lo Zeitgeist (cioè lo «spirito dei tempi») europeo era quello sedimentato da un secolo di cattiva filosofia, specialmente tedesca, e da una guerra disastrosa; e fu in tale ambito che un fisico tedesco ventiquattrenne, Werner Heisenberg, realizzò, nel 1925, un autentico Meisterswerk: organizzò tutti i risultati sperimentali e «teorici» – se quella di Bohr poteva dirsi una «teoria» – secondo tabelle numeriche che risultarono comportarsi come «matrici», oggetti matematici dotati di una loro particolarissima «algebra».
 Questa, sì, era una «teoria»: per quanto complicata e anti-intuitiva, era dotata di coerenza matematica e di capacità sia descrittiva, sia predittiva, e vinse il Nobel nel 1932. Lo stesso Bohr ne rimase conquistato e avvinto, anche se il suo atomo planetario veniva ridotto ad una tabella di numeri simile ad un orario ferroviario. Questa, sì, era una «teoria»: per quanto complicata e anti-intuitiva, era dotata di coerenza matematica e di capacità sia descrittiva, sia predittiva, e vinse il Nobel nel 1932. Lo stesso Bohr ne rimase conquistato e avvinto, anche se il suo atomo planetario veniva ridotto ad una tabella di numeri simile ad un orario ferroviario.
Che c’era di male? Nulla, se non la rinuncia, già in linea di principio, alla costruzione di una teoria che parlasse all’intùito umano, soddisfacendone la creatività visiva e servendosi del suo fondamentale apporto. Dato che i numeri previsti concordavano con l’esperienza, che altro si poteva pretendere, da un «orario ferroviario»? Solo ciò che è «osservabile» ha senso, e ogni altra costruzione dello spirito è una fantasia inutile e arbitraria!
Non ancora sazio, Heisenberg ne trasse un Principio, detto d’Indeterminazione (che probabilmente già gli frullava per la testa all’epoca dei suoi studi liceali, fatti durante la guerra perduta), secondo cui le grandezze fisiche osservabili si presenterebbero in coppie - come la posizione e la velocità di un corpo in moto - che non possono essere misurate con completa precisione nello stesso momento. La precisione dell’una rende imprecisa l’altra, facendo sì che rimanga sempre un limite alla determinazione simultanea di entrambe, e non abbia quindi senso parlare, per esempio, della trajettoria di un corpo, intesa come una precisa sequenza di posizioni e velocità. Dio stesso, per dirla con Einstein, risulterebbe «giocare ai dadi» con una Realtà Fisica che Gli è sfuggita di mano.
La storia non era – per fortuna – finita lì, ma possiamo anticipare che il Principio d’Indeterminazione doveva rimanere annidato nei gangli nervosi della Fisica come un virus, giungendo ancor oggi ad esser visto come la più importante Legge della Fisica, in grado di spiegare tutto, dal Big Bang alla struttura atomica e subatomica, giù giù fino al «vuoto quantico».
 Pochi anni prima (nel 1923), operando, da solo, nel suo palazzo parigino, un nobile francese, il duca Louis de Broglie, aveva avuto un’intuizione formidabile: che non solo le onde elettromagnetiche viaggino per «pacchetti», come previsto da Planck, ma che le particelle materiali viaggino «pilotate» da opportune «onde di materia», di cui egli fu in grado di prevedere la lunghezza d’onda: Pochi anni prima (nel 1923), operando, da solo, nel suo palazzo parigino, un nobile francese, il duca Louis de Broglie, aveva avuto un’intuizione formidabile: che non solo le onde elettromagnetiche viaggino per «pacchetti», come previsto da Planck, ma che le particelle materiali viaggino «pilotate» da opportune «onde di materia», di cui egli fu in grado di prevedere la lunghezza d’onda:
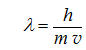 (3) (3)
essendo v la velocità, ed m la massa della particella. L’idea fondamentale di de Broglie era che le leggi della Meccanica Classica (da Newton ad Einstein) siano solo un caso limite di una nuova, più generale «Meccanica Ondulatoria», le cui leggi egli si mise subito a ricercare, abbozzando una sua teoria detta «dell’Onda Pilota».
L’esistenza delle onde di de Broglie fu ben presto confermata sperimentalmente, nel 1927, da Davisson e Germer, mediante la diffrazione di un fascio di elettroni da parte di un cristallo di nickel: un risultato che fruttò il premio Nobel a de Broglie già nel 1929.
 Nel frattempo, seguendo la traccia delle idee di de Broglie, l’equazione descrivente le sue onde di materia fu trovata, nel 1926, da Erwin Schrödinger (premio Nobel 1933). Egli ne trovò, anzi, due (e forse tre). La prima equazione di Schrödinger, detta time-independent (o stazionaria) facilissima da ricavare, è relativa al moto di particelle di energia E, in un potenziale esterno stazionario V(x,y,z), e assume l’aspetto Nel frattempo, seguendo la traccia delle idee di de Broglie, l’equazione descrivente le sue onde di materia fu trovata, nel 1926, da Erwin Schrödinger (premio Nobel 1933). Egli ne trovò, anzi, due (e forse tre). La prima equazione di Schrödinger, detta time-independent (o stazionaria) facilissima da ricavare, è relativa al moto di particelle di energia E, in un potenziale esterno stazionario V(x,y,z), e assume l’aspetto
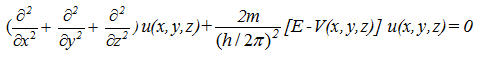 (4) (4)
che riportiamo solo per amore di completezza. Tale equazione differenziale è semplicemente prodigiosa: risulta essere una «equazione agli auto-valori», nel senso che ammette soluzioni (i cosiddetti «auto-stati stazionari», Un(x,y,z) : le onde di de Broglie!) solo per un ben determinato insieme di «auto-valori», (E1, E2,.. En,.. EN), dell’energia. Auto-valori da cui nascono spontaneamente quei "numeri" che formano le complicatissime matrici di Heisenberg: una rivincita dell’intuizione sul formalismo cieco del giovane tedesco, il quale combatté l’approccio ondulatorio con ogni mezzo.
Inutile dire che le intrattabili matrici ebbero, dopo Schrödinger, ben poco sèguito, pur riuscendo a influenzare gli approcci più formali e complicati degli anni a venire.
La seconda equazione di Schrödinger, detta time-dependent, è una semplice conseguenza della prima, e può scriversi nella forma
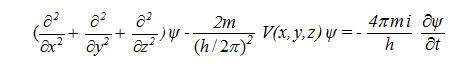 (5) (5)
ove 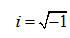 e e 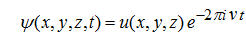 (6) (6)
Non contenendo esplicitamente l’energia, E, delle particelle, l’equazione (5) rappresenta una perdita d’informazione, e non un progresso, rispetto alla (4). Ma pur essendone una conseguenza, essa fu ritenuta più generale, e quindi logicamente più importante, sulla base del fatto che un’espressione della forma
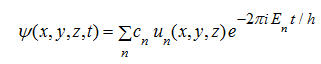 (7) (7)
cioè una sommatoria di tanti termini quanti sono gli auto-valori En della (4), costituisce una soluzione generale della (5), riducendola alla somma di altrettante equazioni stazionarie del tipo (4). Sul ruolo dei coefficienti (costanti) cn torneremo tra poche righe.
E sorgeva un problema: cosa rappresenta tale Ψ?
 Ristagnava ancora, nell’aria avvelenata del primo dopo-guerra, la filosofia indeterministica di Heisenberg, e risultò vincente, quindi, l’interpretazione di Born (Nobel 1954), secondo cui un sistema fisico vive simultaneamente in tutti i suoi auto-stati stazionari Un(x,y,z), fino a quando una nostra misurazione fa collassare (!!) l’energia in un solo «auto-valore», En (quello sperimentalmente osservato), secondo una distribuzione di probabilità determinata dalle quantità Cn2. Ristagnava ancora, nell’aria avvelenata del primo dopo-guerra, la filosofia indeterministica di Heisenberg, e risultò vincente, quindi, l’interpretazione di Born (Nobel 1954), secondo cui un sistema fisico vive simultaneamente in tutti i suoi auto-stati stazionari Un(x,y,z), fino a quando una nostra misurazione fa collassare (!!) l’energia in un solo «auto-valore», En (quello sperimentalmente osservato), secondo una distribuzione di probabilità determinata dalle quantità Cn2.
Dato il ruolo assunto dall’osservatore (cioè da noi!), gli eventi di Natura non possedevano più la realtà obiettiva che i fisici avevano sempre dato per scontata! A questo punto, nello spirito euristico varato anni prima da Bohr, l’equazione (5) venne «generalizzata» nella forma
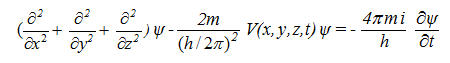 (8) (8)
apparentemente simile alla (5) stessa, ma contenente un potenziale dipendente dal tempo, V(x,y,z,t), al posto di quello indipendente dal tempo, V(x,y,z): il che, come potrebbe mostrarsi agevolmente, rende l’equazione... del tutto ingiustificabile. Mentre la (5) è una facile conseguenza della (4), e quindi, in ultima analisi, dell’ipotesi di de Broglie delle onde di materia, la (8) cade direttamente dal cielo!
La stessa interpretazione di Born, basata sulla (5), pareva ridimensionata...
Ma niente paura: tale terza equazione di Schrödinger fu assunta come dogma, cioè come postulato primario, associato ad una funzione Ψ che, non potendo ritenersi necessariamente della forma (7), diventava, tout court, una descrizione della probabilità di presenza della particella, senza nemmeno potersi più appoggiare su auto-stati stazionari!
Si accettava, seriamente, che delle onde di probabilità (delle onde che potremmo definire «concettuali») potessero viaggiare, interagire con la materia, diffrangere e interferire come onde fisiche, dopo aver tanto predicato sulla natura pragmatica degli «osservabili»!
Le Nuove Leggi della Fisica erano, ora, essenzialmente due:
1) Il Principio d’Indeterminazione, e in posizione subordinata,
2) l’equazione (8).
Era nata – prendendo il nome dalla città ove Bohr era divenuto direttore dell’Istituto di Fisica Teorica danese – la cosiddetta «interpretazione di Copenhagen»: la Meccanica Quantistica per antonomasia. Una Weltanschauung (cioè una «visione del mondo») cui nessuno, da Einstein a Planck, a de Broglie e a Schrödinger, seppe sottrarsi, nonostante i paradossi in cui la Fisica si trovò invischiata (dal leggendario «gatto di Schrödinger» al «paradosso EPR», al «teletrasporto quantico» e ai cosiddetti fenomeni «non-locali»), di cui facciamo grazia al lettore. Paradossi, per altro, di cui i «quantisti» ortodossi erano, e sono, assai più orgogliosi che imbarazzati o pentiti, come se ne traessero un’aura da super-eroi.
La grande astuzia dell’interpretazione di Copenhagen consisteva nell’attribuirsi gli straordinari successi consentiti dalla prima equazione di Schrödinger, asserendo ch’essa è un caso particolare della seconda equazione, e questa della terza. Il contrario esatto del vero!
Purtroppo la classica idea di «trajettorie» delle particelle si era persa per strada: nemmeno le equazioni di Schrödinger parevano in grado di recuperarla, e chi osasse parlarne passava per un retrogrado superstizioso. Il solo a pensarci ancora era de Broglie, ma per non essere estromesso dai salotti, dai congressi, dagli istituti e dalle pubblicazioni dei vincitori, e soprattutto per non giuocarsi il Nobel (di cui era «in odore», per le sue fortunate onde di materia), fu costretto già nel 1927 a ritirare la sua teoria dell’Onda Pilota e ad allinearsi al dogma probabilistico di Copenhagen per i 25 anni successivi.
Da allora in poi ogni tentativo di proporre una visione realistica dei fenomeni fisici che associasse ad un sistema fisico un insieme di variabili – quali posizione e velocità – in grado di descriverlo completamente, venne aborrito come «teoria di variabili nascoste», inutile ed «eretica»...
Il dogma vincente di Heisenberg, Born e Bohr venne poi consolidato da un terroristico «teorema di von Neumann» (1932), che anatemizzava ogni tentativo di sfuggire alla visione probabilistica. Il teorema fu presentato – in tedesco – un anno prima dell’ascesa al potere di Hitler, e quindi in un periodo in cui la gente aveva ben altro cui pensare. E fu dimostrato errato, nel 1964, da J. S. Bell, un fisico del CERN – senza che questo apportasse conseguenza alcuna nell’ambito della comunità scientifica, che rimase, e ancor oggi rimane, saldamente copenhageniana.
 Il solo tentativo di sottrarvisi fu compiuto da David Bohm nel 1952, con l’ambizione di reintrodurre, a dispetto di von Neumann, quelle «variabili nascoste» deterministiche che l’interpretazione di Copenhagen proibiva. Bohm però si fermò a mezza strada, rimanendo ancorato alla visione probabilistica imperante. Egli fornì, in realtà, non già delle vere trajettorie, ma solo, come lui stesso ammise, delle linee di probabilità, in non-disaccordo con Copenhagen – mentre le trajettorie vere e proprie rimanevano un sogno, e paradossi quantistici come la «non-località» restavano invariati. L’approccio di Bohm, sfuggito per poco alla scomunica, risvegliò l’interesse dei chimico-fisici, poco propensi alle elucubrazioni teoriche e più portati alle applicazioni pratiche. Il solo tentativo di sottrarvisi fu compiuto da David Bohm nel 1952, con l’ambizione di reintrodurre, a dispetto di von Neumann, quelle «variabili nascoste» deterministiche che l’interpretazione di Copenhagen proibiva. Bohm però si fermò a mezza strada, rimanendo ancorato alla visione probabilistica imperante. Egli fornì, in realtà, non già delle vere trajettorie, ma solo, come lui stesso ammise, delle linee di probabilità, in non-disaccordo con Copenhagen – mentre le trajettorie vere e proprie rimanevano un sogno, e paradossi quantistici come la «non-località» restavano invariati. L’approccio di Bohm, sfuggito per poco alla scomunica, risvegliò l’interesse dei chimico-fisici, poco propensi alle elucubrazioni teoriche e più portati alle applicazioni pratiche.
E risvegliò pure, dopo 25 anni di torpore, l’orgoglio dell’ormai quasi-sessantenne de Broglie, che ridiscese in campo con i suoi antichi tentativi di definire «variabili nascoste», senza però arrivare a rendersi conto che le equazioni time-dependent di Schrödinger – intrinsecamente probabilistiche – non erano la strada migliore per la costruzione di una dinamica deterministica.
Dopo vari decenni, nel 2007, tre ricercatori operanti presso il DISAA dell’Università di Milano – A. Orefice, R. Giovanelli e D. Ditto (OGD), autori del presente documento – si resero conto, per cominciare, che un famoso luogo comune della Meccanica Classica delle onde andava sfatato.
Da sempre, infatti, l’Ottica andava dicendo che è lecito parlare di «raggi» luminosi solo in un caso (importante, ma limitato): la cosiddetta approssimazione dell’ottica geometrica, valida unicamente per fenomeni di riflessione e rifrazione. In pratica, per prismi, lenti e specchi. Di raggi luminosi – secondo la Vulgata – non si poteva assolutamente parlare per fenomeni come la diffrazione e l’interferenza.
Il gruppo OGD riuscì a dimostrare, invece, che di trajettorie dei raggi si può parlare sempre, pur di tener conto di una funzione contenuta (ma, fino ad oggi, sempre trascurata) nelle abituali equazioni ondulatorie valevoli per onde monocromatiche (cioè di una sola frequenza): una funzione ch’essi denominarono «Wave Potential» (Fig.1, 2).
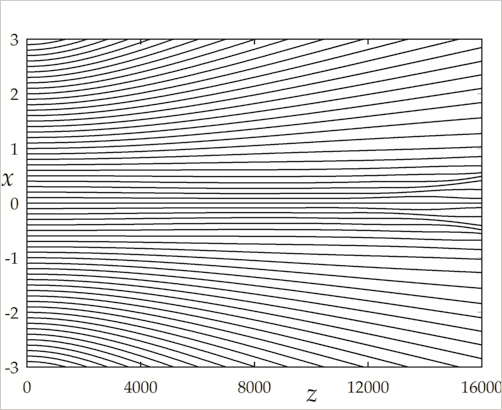
Fig.1 - Fascio di trajettorie nel caso di diffrazione.
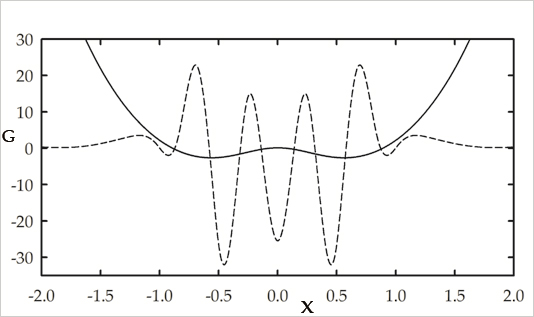
Fig.2 - Profili trasversali iniziale (linea continua) e finale (linea tratteggiata) del Potenziale d’Onda (G) corrispondente alla Fig.1.
È proprio tale funzione a provocare diffrazione e interferenza, agendo perpendicolarmente tra i raggi luminosi – tutt’altro che rettilinei come preteso dalla Vulgata.
Poi il gruppo OGD passò a considerare le onde di de Broglie descritte dalla prima equazione di Schrödinger, scoprendo che le considerazioni fatte nel caso delle onde elettromagnetiche classiche si estendono agevolmente al caso della Meccanica Ondulatoria. Fu anzi semplicissimo estenderle anche al caso relativistico, cui de Broglie aveva sempre pensato.
E sempre si ottenne, senza alcun ricorso a concetti probabilistici, un sistema di trajettorie esatte, cioè un sistema basato, come la Fisica Classica ci aveva abituati a fare, sulle vituperate «variabili nascoste» (posizione e velocità delle particelle) sotto l’azione onnipresente del Wave Potential, che è ciò cui ogni onda – anche un’onda di materia – deve il proprio comportamento.
Come già la Relatività aveva ampliato le leggi della Meccanica Classica, la Meccanica Ondulatoria era ricondotta a leggi dinamiche deterministiche ed esatte ancora più ampie, senza più alcuna traccia di concetti probabilistici.
E l’Indeterminazione? Non c’era più! Si riduceva al fatto – ovvio da sempre – che un’informazione poco precisa porta a risultati poco precisi.
Le particelle avevano ripreso a muoversi lungo sentieri perfettamente determinati, e Dio aveva smesso – se mai n’era stato tentato – di giuocare ai dadi con la Creazione.
Ma, pur dopo la caduta del Muro di Copenhagen, non sarà facile sbrogliare cent’anni di stranezze. Per sradicare la visione tolemaica sono occorsi secoli.
Adriano Orefice, Raffaele Giovanelli e Domenico Ditto
Università degli Studi di Milano - Dipartimento di Scienze Agrarie e Ambientali Produzione, Territorio, Agroenergia (DISAA)
Milano, giugno 2013
Pubblicazioni su riviste internazionali con IF
1) A. Orefice, R. Giovanelli and D. Ditto (2013). A non-probabilistic insight into Wave Mechanics, to appear on the Annales de la Fondation L. de Broglie, Vol. 38.
2) A. Orefice, R. Giovanelli and D. Ditto (2012).Beyond the Eikonal Approximation in Classical Optics and Quantum Physics, in "Applied Bohmian Mechanics: From Nanoscale Systems to Cosmology", ed. by X. Oriols and J. Mompart, Pan Stanford Publishing, Chapt.7 (pg.425-453)
3) A. Orefice, R. Giovanelli and D. Ditto (2009). Complete Hamiltonian Description of Wave-Like Features in Classical and Quantum Physics. Found. Phys. 39, pp. 256-272.
Approfondimenti (*)
1) A. Orefice, R. Giovanelli and D. Ditto (2013). Wave Mechanics without Probability. Published on ArXiv.org. Cite as: arXiv:1302.4247v4 [quant-ph].
2) A. Orefice, R. Giovanelli and D. Ditto (2012). Quantum trajectories and Cushing’s historical contingency. Published on ArXiv.org. Cite as: arXiv:1202.6225v2 [quant-ph].
3) A. Orefice, R. Giovanelli and D. Ditto (2007). Beyond Geometrical Optics and Bohmian Physics: A new exact and deterministic Hamiltonian approach to wave-like features in classical and quantum physics. Published on ArXiv.org. Cite as: arXiv:0705.4049v1 [quant-ph]
(*) Tutta la linea di ricerca è scaricabile online da ArXiv.org (Cornell University Library) al seguente indirizzo web.
 |
Copyright Associazione culturale editoriale EFFEDIEFFE |
|
Nessun commento per questo articolo
Aggiungi commento
|
|
|
|
|
Libreria Ritorno al Reale
EFFEDIEFFESHOP.com
La libreria on-line di EFFEDIEFFE: una selezione di oltre 1300 testi, molti introvabili, in linea con lo spirito editoriale che ci contraddistingue.
|
|
|
|
|
|
Servizi online EFFEDIEFFE.com
|
|
Redazione : Conoscete tutti i collaboratori EFFEDIEFFE.com
|
Contatta EFFEDIEFFE : Come
raggiungerci e come contattarci
per telefono e email.
|
RSS : Rimani aggiornato con i nostri Web feeds
|
|
|
|
|
|
|
Il sito www.effedieffe.com.non è un "prodotto editoriale diffuso al pubblico con periodicità regolare e contraddistinto da una testata", come richiede la legge numero 62 del 7 marzo 2001. Gli aggiornamenti vengono effettuati senza alcuna scadenza fissa e/o periodicità
|
|
|